Accueil / Formules /
Formules
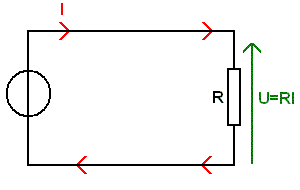
1) Loi d'ohm :
La loi d'ohm se définit par la formule suivante,
U = R x I
U : tension en volt.
R : résistance en ohm.
I : courant en ampère.
2) Relations des puissances :
P = U x I x cos phi
P : puissance active en watt (W).
U : tension en volt.
I : courant en ampère.
cos phi : déphasage entre U et I.
Q = U x I x sin phi
Q : puissance réactive en volt ampère réactif (VAR).
U, I idem que pour P.
sin phi = sinus de inverse cosinus phi.
S = U x I
S : puissance apparente en volt ampère (VA).
U, I idem que pour P et Q.
3) Le déphasage :
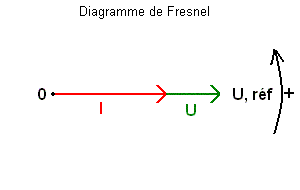
Dans le cas de charge purement résistive, comme le chauffage électrique, l'éclairage incandescent, petit électroménager (cafetière, grille-pain,...), le cos phi est égal à 1, donc il n'y a pas de déphasage entre U et I, l'angle phi est égal à 0.
Le cos phi vaut 1 (cos 0 = 1).
Le sin phi vaut 0 (sin 0 = 0).
Donc P = U x I ; Q = U x I x 0 = 0 ; S = U x I
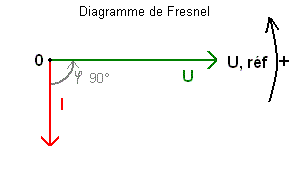
Pour une charge inductive, comme les moteurs, lampes fluorescentes,...etc. La tension est en avance sur le courant, il y a alors déphasage, pouvant aller jusque 90° si la charge est purement inductive (mais en réalité une charge purement inductive n'existe pas).
Le cos phi moyen se situe en général au alentour de 0,8.
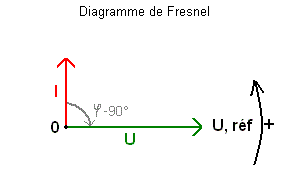
Une charge capacitive entraîne une avance du courant I sur la tension U, la tension U est donc en retard. Une charge capacitive n'est autre qu'un condensateur, il permet de relever le facteur de puissance (cos phi) d'une installation électrique si il est trop bas pour éviter les pénalités de l'EDF car un facteur de puissance trop bas augmente les pertes en ligne, pour corriger cela on installe une batterie de condensateurs.
4) Relations entre les puissances :
Théorème de Boucherot,
Les P et les Q s'additionnent, pas les S.
S= √ (P² + Q²)
Pt = P1 + P2 + P3 +...
Qt = Q1 + Q2 + Q3 +... (attention, dans le cas d'une charge capacitive, il faut mettre le signe moins devant la puissance sachant que de telles charges fournissent de la puissance réactive).
St = √ (Pt² + Qt²)
Autre relation,
K (facteur de puissance) = cos phi = P/S
5) Puissances en triphasé :
Il suffit d'ajouter √3 (racine de 3) aux formules des puissances, ce qui donne :
P = √3 x U x I x cos phi
Q = √3 x U x I x sin phi
S = √3 x U x I
